La relique oubliée traîne dans la bibliothèque de tout informaticien. Tel un écrit sacré, une fois le titre obtenu, elle ne semble plus intéresser son possesseur. Pourtant, tout écart sur la voie inscrite peut être fatal pour l’utilisateur final d’un logiciel écrit par le programmeur. Je parle des Tables de Vérité (TV).
Ce nom résonne pour tout étudiant informatique. Il rappelle un cours ennuyeux sur la logique de Boole. Le nom prêtait à rire. Le reste semblait monotone avec des évidences et des règles déclinées ad nauseam. “Si A et B sont vrais Alors (A et B) est vrai, Si A et faux Alors (A et B) est faux, … “.
Les TV ne sont qu’une façon simplifiée d’écrire ces évidences. Chaque colonne représente un événement (ou une condition) : A, B, … Chaque ligne correspond à une valeur de chaque événement : Vrai ou Faux (0 ou 1, c’est de l’informatique). Une colonne supplémentaire est ajoutée pour exprimer la relation (l’opérateur) entre les deux événements.
Pour les relations ET et OU, nous obtenons les TV suivantes :
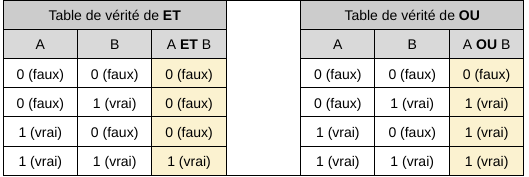
Il est possible de multiplier les événements et les opérateurs pour obtenir des TV dont la complexité augmente au carré du nombre d’événements. Il faut 16 lignes pour exprimer toutes les situations entre les événements A, B, C et D. C’est barbant. Et pour cette raison, les TV sont reléguées au rang de “J’en ai entendu parlé lors des premiers cours d’info”.
La pratique est plus intéressante. Je souhaite jouer au golf. Pour cela il faut que 2 événements soit réalisés :
- A : j’ai terminé mon article
- B : le terrain de golf est ouvert
La TV de ET me donne ainsi toutes les situations où je pourrai pratiquer cette activité. On peut multiplier les événements :
- C : il fait beau
- D : j’ai un parapluie
Je vous laisse calculer la TV de ‘A ET B ET (C OU D)’.
Dans des conditions réelles, il est possible de transiger avec les événements. Mais je ne maîtrise pas les conséquences. Si je joue au golf alors que le terrain est fermé alors j’aurais des problèmes avec le gardien.
Il en est de même avec un programme informatique. Si le développeur n’a pas prévu tous les cas, et donc la bonne règle à contrôler, alors le programme peut avoir des comportements inattendus.
L’erreur classique de logique est lorsqu’on réfléchit par la négative. Pour les événements C et D, leurs opposés sont ‘il ne fait pas beau’ et ‘je n’ai pas de parapluie’. Ils sont alors notés avec un macron, une barre au dessus : Ā. Le caractère n’est pas trouvable, la syntaxe !C est préférée. Pour un non informaticien, je vais écrire nonC.
Il ne fait pas beau devient nonC et je n’ai pas de parapluie devient nonD. Soit S , je sors, le résultat de C et D. Si C OU D Alors S. Écrit plus simplement C OU D = S. Un développeur fainéant qui veut le faire à l’envers écrira nonC OU nonD = non(C OU D) = nonS, je ne sors pas. Regardons les tables de vérité.
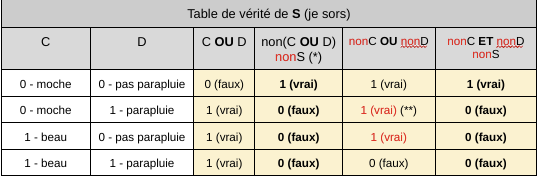
(*) non(C OU D) est l’inverse de (C OU D). Tous les résultats sont inversés.
(**) En rouge, les résultats sont incohérents pour nonS. Il fait beau et je n’ai pas de parapluie, alors je sors. Cela valide le résultat S et non le résultat nonS.
Penser à l’inverse est source d’erreur car non(C OU D) = nonC ET nonD. De même, non(C ET D) = nonC OU nonD.
Lors d’un test pour calculer le prix d’un produit ou vos droits au logement, les conditions (A, B, C, …) sont multipliées. Si le concepteur n’a pas exploré les cas dans une TV, s’il a pensé à l’envers son algorithme, s’il n’a pas rationalisé les conditions, … les risques d’erreurs sont ainsi multipliés.
Pour de nombreux développeurs, les tables de vérité servent à caler des meubles. Ne vous étonnez donc pas si votre logiciel préféré ne réponde pas toujours à vos attentes.
